Introduction
Spring
is defined as an elastic body, whose function is to distort when loaded and to
recover to its original shape when the load is removed.
Objectives of Spring
Following
are the objectives of a spring when used as a machine member:
1. Cushioning,
absorbing, or controlling of energy due to shock and vibration.
Car springs or railway buffers
To control energy, springs-supports and vibration dampers.
2.
Control of motion
Maintaining contact between two elements (cam and its
follower)
In a cam and a follower arrangement,
widely used in numerous applications, a spring maintains contact between the
two elements. It primarily controls the motion.
Creation of the necessary pressure in a friction device (a
brake or a clutch)
A person driving a car uses a brake or
a clutch for controlling the car motion. A spring system keep the brake in
disengaged position until applied to stop the car. The clutch has also got a
spring system (single springs or multiple springs) which engages and disengages
the engine with the transmission system.
Restoration of a machine part to its normal position when
the applied force is withdrawn (a governor or valve)
A typical example is a governor for
turbine speed control. A governor system uses a spring controlled valve to
regulate flow of fluid through the turbine, thereby controlling the turbine
speed.
3.
Measuring forces
Spring balances, gages
4. Storing of energy
In clocks or starters
The clock has spiral type of spring which is wound to coil and then the
stored energy helps gradual recoil of the spring when in operation. Nowadays we
do not find much use of the winding clocks.
Before considering
the design aspects of springs we will have a quick look at the spring materials
and manufacturing methods.
Commonly used spring materials
One of the
important considerations in spring design is the choice of the spring material.
Some of the common spring materials are given below.
·
Hard-drawn wire:
This is cold drawn, cheapest spring steel. Normally used for low stress
and static load. The material is not suitable at subzero temperatures or at
temperatures above 1200C.
·
Oil-tempered wire:
It is a cold drawn, quenched, tempered, and general purpose spring
steel. However, it is not suitable for fatigue or sudden loads, at subzero
temperatures and at temperatures above 1800C.
When we go for highly stressed conditions then alloy steels are useful.
·
Chrome Vanadium:
This alloy spring steel is used for high stress conditions and at high
temperature up to 2200C. It is good for fatigue resistance and long endurance
for shock and impact loads.
·
Chrome Silicon:
This material can be used for highly stressed springs. It offers
excellent service for long life, shock loading and for temperature up to 2500C.
·
Music wire:
This spring material is most widely used for small springs. It is the
toughest and has highest tensile strength and can withstand repeated loading at
high stresses. However, it can not be used at subzero temperatures or at
temperatures above 1200C.
Normally when we talk about springs we will find that the music wire is
a common choice for springs.
·
Stainless steel:
Widely used alloy spring materials.
·
Phosphor Bronze /
Spring Brass:
It has good corrosion resistance and electrical conductivity. That’s the
reason it is commonly used for contacts in electrical switches. Spring brass
can be used at subzero temperatures.
Spring
manufacturing processes
If springs are of
very small diameter and the wire diameter is also small then the springs are
normally manufactured by a cold drawn process through a mangle. However, for
very large springs having also large coil diameter and wire diameter one has to
go for manufacture by hot processes. First one has to heat the wire and then
use a proper mangle to wind the coils.
Helical spring
The figures below show the schematic representation
of a helical spring acted upon by a tensile load F (Fig.7.1.1) and compressive
load F (Fig.7.1.2). The circles denote the cross section of the spring wire.
The cut section, i.e. from the entire coil somewhere we make a cut, is
indicated as a circle with shade.
If we
look at the free body diagram of the shaded region only (the cut section) then
we shall see that at the cut section, vertical equilibrium of forces will give
us force, F as indicated in the figure. This F is the shear force. The torque
T, at the cut section and it’s direction is also marked in the figure. There is
no horizontal force coming into the picture because externally there is no
horizontal force present. So from the fundamental understanding of the free
body diagram one can see that any section of the spring is experiencing a
torque and a force. Shear force will always be associated with a bending
moment.
However, in an ideal situation, when force is acting at the
centre of the circular spring and the coils of spring are almost parallel to each
other, no bending moment would result at any
section of the spring ( no moment arm), except torsion and
shear force. The Fig.7.1.3 will explain the fact stated above.
Stresses
in the helical spring wire:
From the free body diagram, we have found out the direction
of the internal torsion T and internal shear force F at the section due to the
external load F acting at the centre of the coil.
The cut sections of the spring, subjected to tensile and
compressive loads respectively, are shown separately in the Fig.7.1.4 and
7.1.5. The broken arrows show the shear stresses ( τT )
arising due to the torsion T and solid arrows show the shear stresses ( τF ) due
to the force F. It is observed that for both tensile load as well as
compressive load on the spring, maximum shear stress (τT + τF)
always occurs at the inner side of the spring. Hence, failure of the spring, in
the form of crake, is always initiated from the inner radius of the spring.
The radius
of the spring is given by D/2. Note that D is the mean diameter of the spring.
The torque T acting on the spring is
(7.1.1)
If d is the diameter of the coil wire
and polar moment of inertia the shear stress in the spring wire due to torsion
is
Average
shear stress in the spring wire due to force F is
Therefore, maximum shear stress the
spring wire is
The above equation gives maximum shear
stress occurring in a spring. Ks is the shear stress correction
factor.
Stresses in
helical spring with curvature effect:
What is curvature effect? Let us look at a small section of a
circular spring, as shown in the Fig.7.1.6. Suppose we hold the section b-c
fixed and give a rotation to the section a-d in the anti clockwise direction as
indicated in the figure, then it is observed that line a-d rotates and it takes
up another position, say a'-d'. The inner length a-b being smaller compared to
the outer length c-d, the shear strain γi at the inside of the spring
will be more than the shear strain γo at the outside of the spring.
Hence, for a given wire diameter, a spring with smaller diameter will
experience more difference of shear strain between outside surface and inside
surface compared to its larger counter part. The above phenomenon is termed as
curvature effect. So more is the spring index (C=D/d) the lesser will be the
curvature effect. For example, the suspensions in the railway carriages use
helical springs. These springs have large wire diameter compared to the
diameter of the spring itself. In this case curvature effect will be
predominantly high.
To take care of the curvature effect, the earlier equation
for maximum shear stress in the spring wire is modified as,
Where,
KW is
Wahl correction factor, which takes care of both curvature effect and shear
stress correction factor and is expressed as,
Deflection
of helical spring:
Consider
a small segment of spring of length ds, subtending an angle of dβ at the center
of the spring coil as shown in Fig.7.1.7(b). Let this small spring segment be
considered to be an active portion and remaining portion is rigid. Hence, we
consider only the deflection of spring arising due to application of force F.
The rotation, dφ, of the section a-d with respect to b-c is given as,
The
rotation, dφ will cause the end of the spring O to rotate to O', shown in Fig. 7.1.7(a).
From geometry, O-O' is given as,
However,
the vertical component of O-O' only will contributes towards spring deflection.
Due to symmetric condition, there is no lateral deflection of spring, ie, the
horizontal component of O-O' gets cancelled.
The vertical component of O-O', dδ, is
given as,
Total
deflection of spring, δ, can be obtained by integrating the above
expression for entire length of the spring wire.
Simplifying
the above expression we get,
Where,
N is the number of active turns and G is the shear modulus of
elasticity. Now what is an active coil? The force F cannot just hang in space,
it has to have some material contact with the spring. Normally the same spring
wire e will be given a shape of a hook to support the force F. The hook etc.,
although is a part of the spring, they do not contribute to the deflection of
the spring. Apart from these coils, other coils which take part in imparting
deflection to the spring are known as active coils.
The
above equation is used to compute the deflection of a helical spring. Another
important design parameter often used is the spring rate. It is defined as,
Here
we conclude on the discussion for important design features, namely, stress,
deflection and spring rate of a helical spring.
Design
of helical spring for variable load
In
the case of a spring, whether it is a compression spring or an extension
spring, reverse loading is not possible. For example, let us consider a
compression spring placed between two plates. The spring under varying load can
be compressed to some maximum value and at the most can return to zero
compression state (in practice, some amount of initial compression is always
present), otherwise, spring will loose contact with the plates and will get
displace from its seat. Similar reason holds good for an extension spring, it
will experience certain amount of extension and again return to at the most to
zero extension state, but it will never go to compression zone. Due to varying
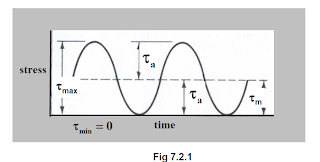
load, the stress pattern which occurs in a spring with respect to time is shown
in Fig.7.2.1. The load which causes such stress pattern is called repeated
load. The spring materials, instead of testing under reversed bending, are
tested under repeated torsion.
From
Fig.7.2.1 we see that,
Where,
τa is
known as the stress amplitude and τm is known as the mean stress
or the average stress. We know that for varying stress, the material can
withstand stress not exceeding endurance limit value. Hence, for repeated
torsion experiment, the mean stress and the stress amplitude become,
(7.2.2)
Soderberg
failure criterion :
The modified Soderberg diagram for repeated stress is shown
in the Fig 7.2.2.
The stress
being repeated in nature, the co-ordinate of the point a is ( τe/2, τe/2). For safe
design, the design data for the mean and average stresses, τa and τm respectively, should
be below the line a-b. If we choose a value of factor of safety (FS), the line
a-b shifts to a newer position as shown in the figure. This line e-f in the
figure is called a safe stress line and the point A (τm,τa) is a typical safe design point.
Considering
two similar triangles, abc and Aed respectively, a relationship
between the stresses may be developed and is given as,
where
τY is
the shear yield point of the spring material.
In simplified form, the equation for
Soderberg failure criterion for springs is
The
above equation is further modified by considering the shear correction factor,
Ks and
Wahl correction factor, Kw. It is a normal practice to multiply τm by Ks and to
multiply τa
by Kw.
The above equation for Soderberg
failure criterion for will be utilized for the designing of springs subjected
to variable load.
Estimation
of material strength
It is
a very important aspect in any design to obtain correct material property. The
best way is to perform an experiment with the specimen of desired material.
Tensile test experiments as we know is relatively simple and less time
consuming. This experiment is used to obtain yield strength and ultimate
strength of any given material. However, tests to determine endurance limit is
extremely time consuming. Hence, the ways to obtain material properties is to
consult design data book or to use available relationships, developed through
experiments, between various material properties. For the design of springs, we
will discuss briefly, the steps normally used to obtain the material
properties.
One of the relationships to find out
ultimate strength of a spring wire of diameter d is,
For some selected materials,
which are commonly used in spring design, the values of As and ms are
given in the table below.
The
above formula gives the value of ultimate stress in MPa for wire diameter in
mm. Once the value of ultimate strength is estimated, the shear yield strength
and shear endurance limit can be obtained from the following table developed
through experiments for repeated load.
Hence,
as a rough guideline and on a conservative side, values for shear yield point
and shear endurance limit for major types of spring wires can be obtained from
ultimate strength as,
With
the knowledge of material properties and load requirements, one can easily
utilize Soderberg equation to obtain spring design parameters.
Types
of springs
There are mainly two types of helical springs, compression
springs and extension springs. Here we will have a brief look at the types of
springs and their nomenclature.
1. Compression springs
Following are the types of compression
springs used in the design.
In the
above nomenclature for the spring, N is the number of active coils,
i.e., only these coils take part in the spring action. However, few other coils
may be present due to manufacturing consideration, thus total number of coils, NT may
vary from total number of active coils.
Solid
length, LS
is that length of the spring, when pressed, all the spring
coils will clash with each other and will appear as a solid cylindrical body.
The
spring length under no load condition is the free length of a spring.
Naturally, the length that we visualise in the above diagram is the free length.
Maximum amount of compression the
spring can have is denoted as δmax, which is calculated from the design
requirement. The addition of solid length and the δmax should be sufficient
to get the free length of a spring. However, designers consider an additional
length given as δ allowance. This allowance is provided to avoid clash
between to consecutive spring coils. As a guideline, the value of δ allowance is
generally 15% of δmax.
The
concept of pitch in a spring is the same as that in a screw.
The top and
bottom of the spring is grounded as seen in the figure. Here, due to grounding,
one total coil is inactive.
In
the Fig 7.2.5 it is observed that both the top as well as the bottom spring is
being pressed to make it parallel to the ground instead of having a helix
angle. Here, it is seen that two full coils are inactive.
It
is observed that both the top as well as the bottom spring, as earlier one, is
being pressed to make it parallel to the ground, further the faces are grounded
to allow for proper seat. Here also two full coils are inactive.
2. Extension
springs
Part
of an extension spring with a hook is shown in Fig.7.2.7. The nomenclature for
the
extension spring is given below.
Body length, LB: d
(N + 1)
Free length, L : LB +
2 hook diameter.
here, N stands for the number of active
coils. By putting the hook certain amount of stress concentration comes in the
bent zone of the hook and these are substantially weaker zones than the other
part of the spring. One should take up steps so that stress concentration in
this region is reduced. For the reduction of stress concentration at the hook
some of the modifications of spring are shown in Fig 7.2.8.
Buckling
of compression spring
Buckling is an instability that is normally shown up when a
long bar or a column is applied with compressive type of load. Similar
situation arise if a spring is too slender and long then it sways sideways and
the failure is known as buckling failure. Buckling takes place for a
compressive type of springs. Hence, the steps to be followed in design to avoid
buckling is given below.
Free length (L) should be less than 4 times the coil
diameter (D) to avoid buckling for most situations. For slender springs central
guide rod is necessary.
A guideline
for free length (L) of a spring to avoid buckling is as follows,
For steel,
Where, Ce is
the end condition and its values are given below
Ce End condition
2.0 fixed and free
end
1.0 hinged at both
ends
0.707 hinged and fixed end
0.5 fixed at both ends
If
the spring is placed between two rigid plates, then end condition may be taken
as 0.5. If after calculation it is found that the spring is likely to
buckle then one has to use a guide rod passing through the center of the spring
axis along which the compression action of the spring takes place.
Spring surge (critical frequency)
If a
load F act on a spring there is a downward movement of the spring and due to
this movement a wave travels along the spring in downward direction and a to
and fro motion continues. This phenomenon can also be observed in closed water
body where a disturbance moves toward the wall and then again returns back to
the starting of the disturbance. This particular situation is called surge of
spring. If the frequency of surging becomes equal to the natural frequency of
the spring the resonant frequency will occur which may cause failure of the
spring. Hence, one has to calculate natural frequency, known as the fundamental
frequency of the spring and use a judgment to specify the operational frequency
of the spring.
The fundamental frequency can be
obtained from the relationship given below.
Fundamental
frequency :
 Both ends within
flat plates
One
end free and other end on flat plate.
Both ends within
flat plates
One
end free and other end on flat plate.
Where,
K: Spring rate
 WS :
Spring weight =
WS :
Spring weight =
and d is
the wire diameter, D is the coil diameter, N is the number of
active coils and γ is the specific weight of spring material.
The
operational frequency of the spring should be at least 15-20 times less than
its fundamental frequency. This will ensure that the spring surge will not
occur and even other higher modes of frequency can also be taken care of.
Spring Manufacturing Process